Efekt Comptona

Zjawisko Comptona polega na rozpraszaniu fotonów o wysokiej energii na swobodnych lub słabo związanych elektronach. Obiektami rozpraszającymi są tarcze w kształcie walców wykonanych z aluminium, miedzi albo grafitu. W doświadczeniu obserwuje się zmianę energii rozproszonych kwantów promieniowania w funkcji kąta rozproszenia. Celem doświadczenia jest weryfikacja wzoru Comptona oraz wyznaczenie energii początkowej rozpraszanych fotonów.

Wymagania

1. Rozpady promieniotwórcze – ścieżka stabilności.
2. Rozpady promieniotwórcze i ich rodzaje (klasyfikacja przemian promieniotwórczych).
3. Prawo spontanicznego rozpadu promieniotwórczego, aktywność źródła, stała rozpadu, prawdopodobieństwo rozpadu.
4. Podstawowe wiadomości dotyczące przemian α, β, γ (krótka charakterystyka tych rodzajów promieniowania).
5. Powstawanie promieniowania γ.
6. Oddziaływanie promieniowania γ z materią (wymień najważniejsze zjawiska i podaj ich krótką charakterystykę).
7. Podstawowe wielkości i jednostki używane w ochronie radiologicznej (w szczególności: aktywność, dawka ekspozycyjna, dawka pochłonięta, równoważnik dawki, efektywny równoważnik dawki).
8. Wyjaśnij na czym polega oddziaływanie promieniowania jonizującego na komórki.
9. Omów zjawisko Comptona.
10. Wyprowadź wzór na comptonowską zmianę długości fali.
11. Oblicz jaka jest długość fali fotonu γ rozproszonego “comptonowsko” pod kątem 90° dla promieniowania emitowanego przez jądra cezu ¹³⁷Cs. Jak duża (procentowo) jest zmiana długości fali w stosunku do długości fali początkowej? Oblicz jaka jest energia rozproszonego fotonu γ. Dane potrzebne do obliczeń znajdź w tablicach.
12. Przeprowadź analogiczne, jak w poprzednim punkcie, obliczenia dla linii charakterystycznej promieniowania X (linia K_α molibdenu).
13. Na czym polega zjawisko scyntylacji? W jaki sposób promieniowanie γ oddziałuje ze scyntylatorem (wymień i omów najważniejsze zjawiska). Wymień i omów przynajmniej dwa typy luminescencji, z którymi można mieć do czynienia w scyntylatorach.
14. Zasada działania wielokanałowego analizatora amplitudy impulsów elektrycznych.

Aparatura i materiały

W zadaniu wykorzystuje się:

• sondę scyntylacyjną SSU-70-2 (SS),
• wzmacniacz liniowy WL-21 (W),
• zasilacz fotopowielacza sondy ZWN-41 (ZWN),
• analizator wielokanałowy TUKAN-8k (A) sprzężony z komputerem (PC) przez złącze USB,
• źródło promieniowania γ (¹³⁷Cs, energia kwantów E_γ = 0,662 MeV).

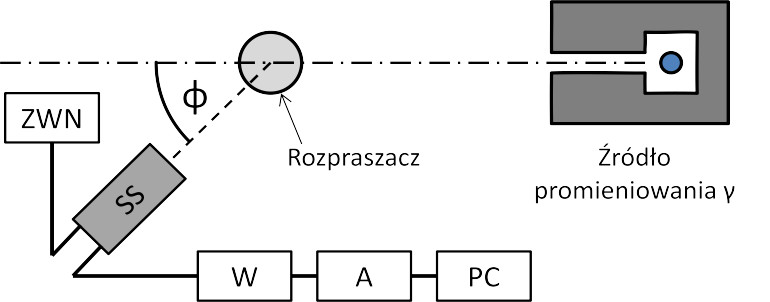
Rys. 1. Schemat aparatury. Oznaczenia: SS – sonda scyntylacyjna, ZWN – zasilacz wysokiego napięcia (zasilacz fotopowielacza sondy), W – wzmacniacz, A – analizator wielokanałowy, PC – komputer, φ – kąt rozproszenia

Zasilacz ZWN-41 jest wbudowany w kasetę pomiarową systemu STANDARD-70 i dostarcza wysokie napięcie do zasilania sondy scyntylacyjnej (+980 V) oraz napięcie +24 V do zasilania przedwzmacniacza sondy.. W wolnym gnieździe kasety umieszczony jest wzmacniacz liniowy WL-21. Analizator wielokanałowy TUKAN-8k jest zasilany z komputera przez złącze USB.

Włączenie aparatury (odbywa się pod nadzorem opiekuna)

1. Ustawić polaryzację wysokiego napięcia na zasilaczu ZWN-41 na “0”
2. Włączyć zasilacz wysokiego napięcia ZWN-41 oraz komputer PC.
3. Ustawić napięcie zasilania sondy scyntylacyjnej (+980 V).
4. Ustawić polaryzację wysokiego napięcia na zasilaczu ZWN-41 na “+”
5. Wywołać program obsługi analizatora TUKAN-8k.
6. Zapoznać się z instrukcją obsługi analizatora wielokanałowego (ustawienie parametrów pracy, rejestracja widma, zapis widma na dysk).

Wykonanie pomiarów

1. W programie TUKAN-8k ustawić czas rejestracji widm na 300s.
2. Z obudowy źródła promieniowania wyjąć zatyczkę blokującą wiązkę promieniowania gamma. UWAGA! NIE WOLNO “zaglądać” do wnętrza obudowy źródła promieniowania ani umieszczać na drodze wiązki jakiejkolwiek części ciała.
3. Na drodze wiązki promieniowania umieszczać kolejno walec aluminiowy, miedziowy i grafitowy (pełnią one funkcję rozpraszacza – rys.1.). Podczas wymiany rozpraszacza każdorazowo umieszczać zatyczkę blokującą wiązkę promieniowania. Dla każdego z rozpraszaczy rejestrować widma amplitudowe scyntylacji (liczba zliczeń fotonów gamma w funkcji numeru kanału analizatora) powstałe w wyniku oddziaływania monoenergetycznego promieniowania γ ze scyntylatorem. Pomiary wykonać dla kątów od 0° do 120°, z krokiem 15° dla zakresu 0° – 90° i z krokiem 30° dla zakresu 90° – 120°.
4. Po każdym pomiarze zapisywać widmo na dysk komputera.
5. Po zakończeniu wszystkich pomiarów przenieść dane pomiarowe na zewnętrzny nośnik danych.

Sprawozdanie

Sprawozdanie powinno zawierać wykresy wykonanych pomiarów, analizę zmian położenia piku fotoelektrycznego w funkcji kąta dla wszystkich rozpraszaczy, analizę niepewności pomiarowych. Dobrym przykładem takiej analizy może być np. opis w [13].

Literatura

1. A. H. Compton, A Quantum Theory of the Scattering of X-rays by Light Elements, Phys. Rev., 21, 483 (1923).
2. Arthur H. Compton, X-rays as a branch of optics, Wykład Noblowski, 12. grudnia 1927.
3. Ewa Skrzypczak, Zygmunt Szefliński. Wstęp do fizyki jądra atomowego i cząstek elementarnych. Wydawnictwo Naukowe PWN, Warszawa 1995.
4. Adam Strzałkowski. Wstęp do fizyki jądra atomowego. Państwowe Wydawnictwo Naukowe, Warszawa 1979.
5. Janusz Araminowicz, Krystyna Małuszyńska, Marian Przytuła, Laboratorium fizyki jądrowej. PWN Warszawa 1978.
6. J.B.A. England, Liczniki scyntylacyjne. In: Metody doświadczalne fizyki jądrowej, PWN Warszawa 1980, s. 50-80.
7. A. Bernstein and A. K. Mann, Summary of Recent Measurements of the Compton Effect, Am. J. Phys. 24, 445 (1956).
8. Albert Allen Bartlett, Compton Effect: Historical Background, Am. J. Phys. 32, 120 (1964).
9. Albert Allen Bartlett, Compton Effect: A Simple Laboratory Experiment, Am. J. Phys. 32, 127 (1964).
10. A. A. Bartlett, J. H. Wilson, O. W. Lyle, Jr., C. V. Wells, and J. J. Kraushaar, Compton Effect: an Experiment for the Advanced Laboratory, Am. J. Phys. 32, 135 (1964).
11. J. Higbie, Undergraduate Relativity Experiment, Am. J. Phys. 42, 642 (1974).
12. R. P. Singhal and A. J. Burns, Verification of Compton collision and Klein-Nishina formulas.an undergraduate laboratory experiment, Am. J. Phys. 46, 646 (1978).
13. A. Melissinos, Experiments in Modern Physics, Academic Press, 1966.